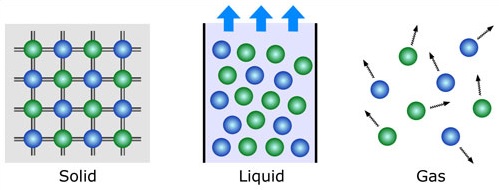
통계 물리 – 많은 수의 미시적인 개체들이 일으키는 거시적인 현상을 탐구
소수의 개체들로 구성된 하나의 계를 생각해보자. 우리는 개체들간의 상호작용을 통해 나타나는 운동 방정식을 풀이함으로써 이 계에서 나타나는 현상을 이해할 수 있다. 하지만 개체들의 개수가 매우 많아지게 된다면 어떻게 될까? 이러한 기존 방식의 접근법은 매우 많은 양의 계산량을 요구하기 때문에 계의 거시적인 성질을 이해하기 위해서는 새로운 접근법이 필요하다. 통계 물리는 이러한 질문에 답하기 위해 계가 보일 수 있는 상태들을 확률 및 통계적으로 접근함으로써 그 해답을 찾고자 하였다.
매우 많은 수의 개체들로 구성된 계의 대표적인 예로 기체를 생각해볼 수 있다. 가시적인 크기의 기체를 구성하는 기체 분자의 수는 〖10〗^23개에 비례하는 것으로 알려져 있다. 사람들은 경험적으로 기체에서 나타나는 온도, 부피, 밀도, 압력과 같은 성질들이 보이는 열역학을 이해하고 있었다. 통계 물리는 이러한 거시적인 열역학을 미시적인 관점에서 이해하기 위해 기체 분자들의 운동을 확률적으로 접근함으로써, 둘 사이의 관계를 성공적으로 설명할 수 있었다. 또한 기체분자들 사이의 상호작용 힘을 통해 기체-액체 상전이를 미시적인 관점에서 이해할 수 있게 되었다. 이러한 성공적인 이론적 틀을 바탕으로 현재 통계 물리는 물리의 독자적인 한 분야를 구축하고 있다.
통계 물리학은 기체와 같은 많은 개체들로 구성된 계를 다루던 기존의 방법론을 활용해서 현재 응집 물질, 생물계, 사회 경제계 등에서 학제간 연구를 활발하게 수행하고 있다. 많은 연구성과를 통해 다양한 분야의 이해를 돕고 있으며, 전산적 기술 발달에 힘입어 앞으로 더욱더 큰 역할을 담당할 수 있을 것이라고 기대한다.
매우 많은 수의 개체들로 구성된 계의 대표적인 예로 기체를 생각해볼 수 있다. 가시적인 크기의 기체를 구성하는 기체 분자의 수는 〖10〗^23개에 비례하는 것으로 알려져 있다. 사람들은 경험적으로 기체에서 나타나는 온도, 부피, 밀도, 압력과 같은 성질들이 보이는 열역학을 이해하고 있었다. 통계 물리는 이러한 거시적인 열역학을 미시적인 관점에서 이해하기 위해 기체 분자들의 운동을 확률적으로 접근함으로써, 둘 사이의 관계를 성공적으로 설명할 수 있었다. 또한 기체분자들 사이의 상호작용 힘을 통해 기체-액체 상전이를 미시적인 관점에서 이해할 수 있게 되었다. 이러한 성공적인 이론적 틀을 바탕으로 현재 통계 물리는 물리의 독자적인 한 분야를 구축하고 있다.
통계 물리학은 기체와 같은 많은 개체들로 구성된 계를 다루던 기존의 방법론을 활용해서 현재 응집 물질, 생물계, 사회 경제계 등에서 학제간 연구를 활발하게 수행하고 있다. 많은 연구성과를 통해 다양한 분야의 이해를 돕고 있으며, 전산적 기술 발달에 힘입어 앞으로 더욱더 큰 역할을 담당할 수 있을 것이라고 기대한다.